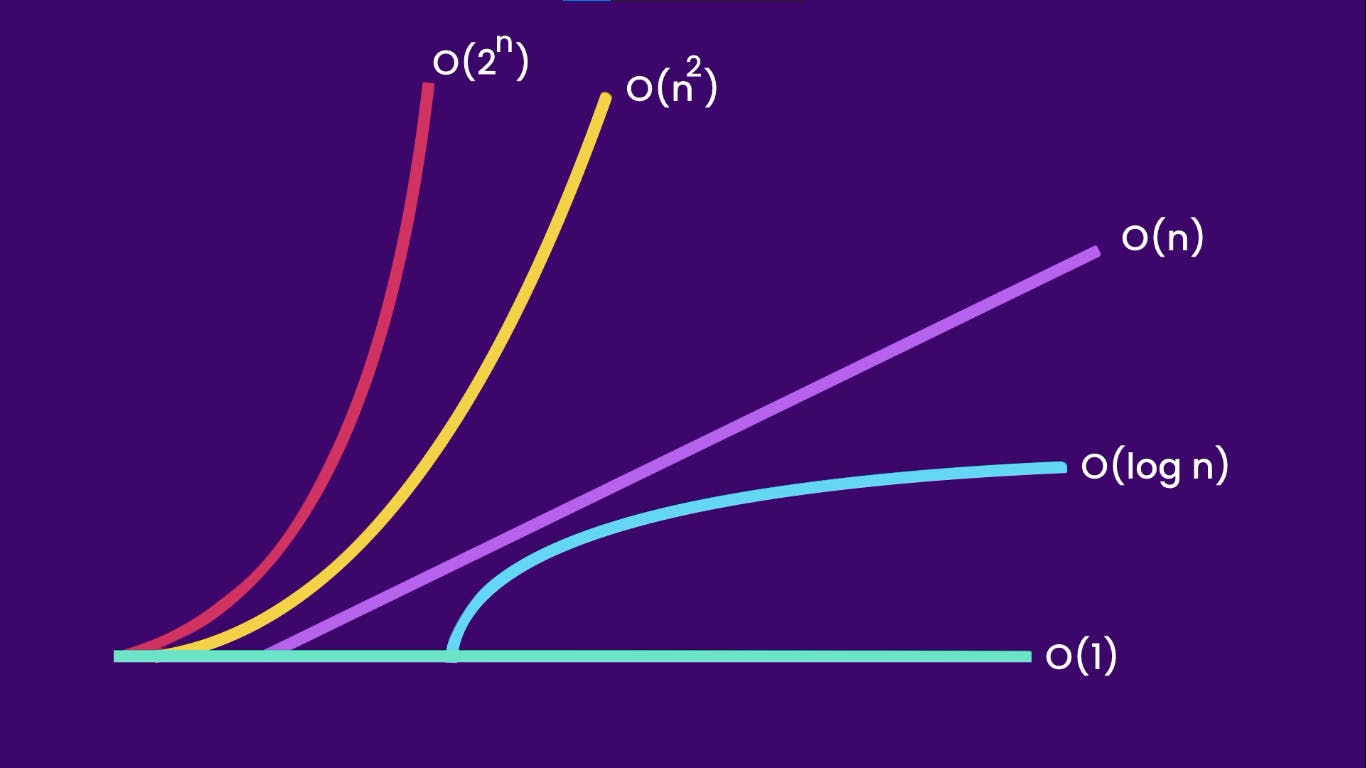
First of all, what is Big O?
It is the way of determining the performance of algorithms as the input grows bigger and bigger. In other words, how much time and space the algorithm would take to execute as the input grows larger.
Why should we care?
Big O is needed so that we can optimize code so that it would deliver fast performance even when millions of people are using the application at the same time. Also, it is very important to know about Big-O in technical interviews.
Let's talk about time complexity:
Time complexity describes that how the time required to execute an algorithm varies with respect to the size of the input.
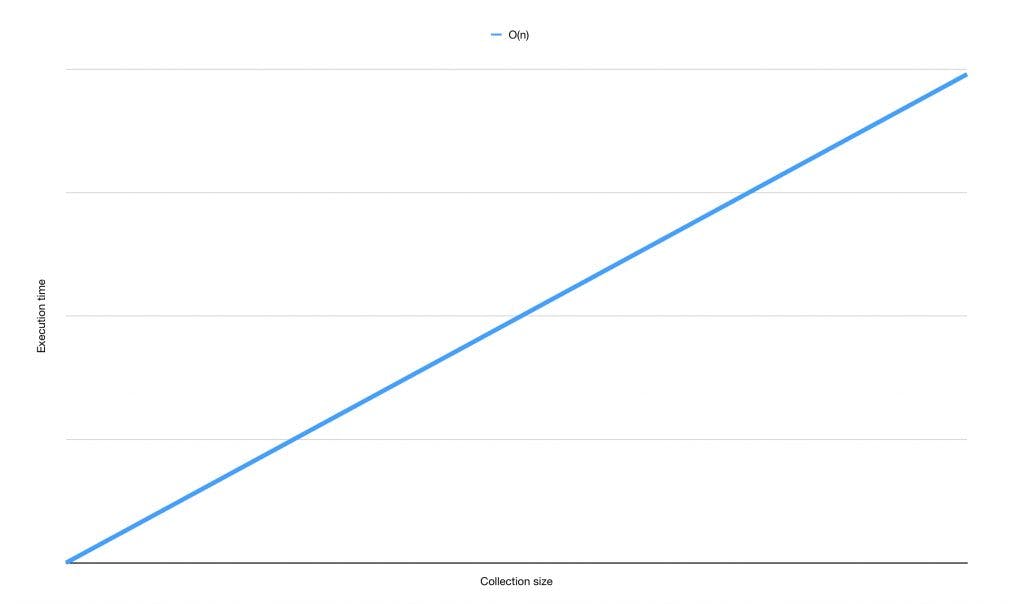
O(n) time complexity
Look at the code below 👇 (language: JavaScript)

In the above function, the for loop will run 'n' times, so as the input(n) grows, the algorithm would have to undergo more iterations, and hence taking more time. So the size of the input(n) is directly proportional to the time taken to run the code. This is called O(n) time complexity and the graph looks like this:
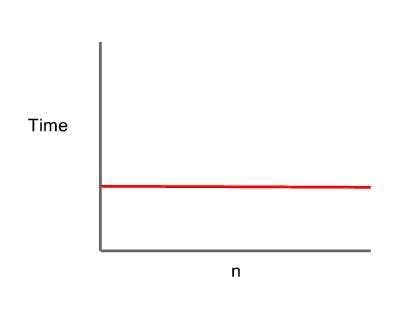
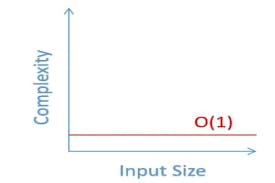
O(1) time complexity
Now, look at the code below 👇

In the above code, the function takes in an array and prints its first element. So here this code will take a constant amount of time to run irrespective of the size of the array. That means there is no relation between input size and execution time. This is called O(1) type complexity, where the algorithm takes a constant amount of time to run and the graph looks like this:
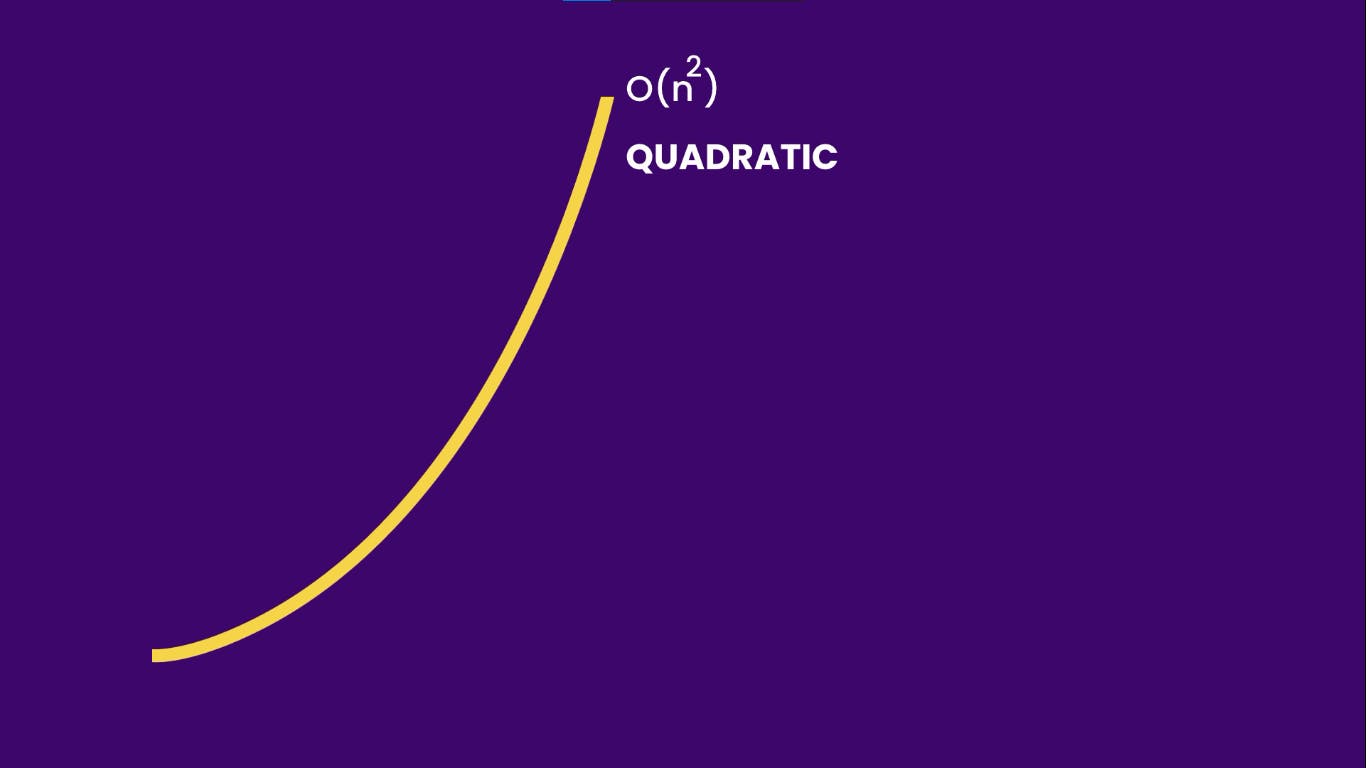
O(n²) time complexity
Let's move on to O(n²), look at the code below:

The function above takes an input(n) and prints all the pairs of numbers that add up and make 'n'. Here we are using nested loops, so, there are n iterations of the outer loop and for each iteration of the outer loop, there are n iterations of the inner loop. That makes the total iterations to:
n * n = n²
that is why it is called O(n²) type complexity because as n grows the time required to execute the algorithm grows exponentially(raised to the power of 2) because of the growth in iterations.
The graph looks like this:
Space Complexity
Now let's talk space complexities:
Space complexity is defined as the extra space required by the algorithm to execute apart from the space required for input. In other words, how much memory an algorithm takes to execute. Some things to note before moving:
Most primitive data types(booleans, numbers, undefined, null) roughly take the same amount of space irrespective of their value. for example:
x = 10 and x = 100000 would take the same amount of memory.
Same in the case of booleans:
isTall = true isTall = false
both isTall variables require the same amount of storage.
But strings require O(n) space where n is the string length.
for example:
x = '1' y = '123456789'
here y would take 9 times more space than x because it has 9 characters and x has only one. Reference types generally require O(n) space where n is the length (for arrays) or the number of keys (for objects).
for example:
x = [1] y = [1, 2]
here y takes twice as much space as x because its length is 2 times that of x.
O(1) Space Complexity
Now, look at the code below 👇

The function above takes an array and return the sum of all the items in the array. Now we have to figure out how much space the algorithm takes to execute. Here we have two variables, 'total' and 'i'(in the for loop). That's all it is, there are only two variables whose space requirement would always be the same no matter the size of the array.
This type of space complexity is called O(1) where the space is constant irrespective of input size. The graph looks the same as O(1) time complexity.
O(n) Space Complexity
Now, look at the code below 👇

The function above takes an array as an input and return a new array with all the elements double of the elements in the input array.
we have two variables here 'i' (in for loop) and 'newArr'(the array that is returned) The space requirement of 'i' is always the same, but that of 'newArr' increases as the length of the input array increases, because 'newArr' would be of the same length as the input array and as the length of arrays increase, so does their size.
So input size is directly proportional to space requirement, this type of space complexity is called O(n) and the graph looks exactly the same as that of O(n) time complexity.
In conclusion, execution time and space requirement order of algorithms:
O(n²) > O(n) > O(1)
that means O(n²) algorithms are slowest and becomes more and more space-intensive as the input size grows while O(1) algorithms are fastest and require a constant space to run. Here is a cheat sheet for you to remember graphs of different types of complexities 👇